What is multiple linear regression?

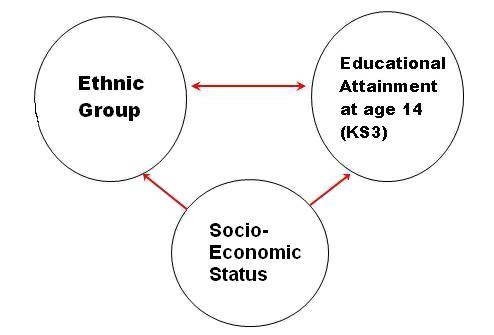
In the previous module we saw how simple linear regression could be used to predict the value of an outcome variable based on the value of a suitable explanatory variable. This is a useful technique but it is limited - usually a number of different variables will predict an outcome. For example, how good a student is at football is not just related to how many hours they practice a week. There is likely to be a relationship between ability and practice but discussing this in isolation from other important variables would most likely be a considerable over-simplification. The young player’s spatial-awareness and physical fitness are also likely to contribute to their overall level of ability. Their ability may partly stem from personality traits that are related to confidence and teamwork.

Of course we can go even further than this and say that sometimes the explanatory variables can influence each other as well as the outcome itself! For example, the impact of training on ability is bound to be dependent on the level of motivation the student feels. Perhaps they are turning up to training but not putting any effort in because they don’t really like football! The real world is very complicated but luckily, with regression analysis, we can at least partially model that complexity to gain a better understanding. Multiple linear regression (MLR) allows the user to account for multiple explanatory variables and therefore to create a model that predicts the specific outcome being researched. Multiple linear regression works in a very similar way to simple linear regression.

Consider the example of understanding educational attainment. It is well known that there is a strong and positive correlation between social class and educational attainment. There is evidence that pupils from some (though not all) minority ethnic groups do not achieve as well in the English education system as the majority White British group. However there is also a strong relationship between ethnic group and social class, with many minority ethnic groups experiencing higher socio-economic disadvantage than the White British group. It is therefore not possible to say from raw scores alone whether the lower attainment of some minority ethnic groups reflects something particular about belonging to that ethnic group or reflects the fact that some ethnic groups are particularly socially and economically disadvantaged. The relationship may look a little like the one presented below (Figure 2.1.1).

Figure 2.1.1: The third variable problem

Multiple regression offers a way to address these issues. If we put all the variables we have into one analysis, we can assess the impact of one factor when another is taken into account. Thus multiple regression can allow us to assess the association of ethnicity and attainment after the variance in attainment associated with social class is taken into account. A wide range of further variables can also be included to build up highly detailed and complex models, e.g. family composition, maternal educational qualifications, students’ attitude to school, parents educational aspirations for the student, etc.

Running through the examples and exercises using SPSS

As in the previous module, we provide worked examples from LSYPE which you can follow through using SPSS. You will find that we make a lot of transformations to the dataset as we perform the various analyses. It could get confusing! We recommend that you do not make the transformations yourself (one small error could dramatically alter your output) and instead use the pre-prepared variables in the MLR LSYPE 15,000 dataset. However if you really do want to perform all of the transformations yourself you can always use the original LSYPE 15,000 data file. Both are available below or from our Resources pages.

MLR LSYPE 15,000

LSYPE 15,000

Navigation

Home
Modules
Site Guide
Module 3 Contents
Resources