The final version of the model

In all the models we have computed so far we have not included the variable which we saw in the SLR module had the biggest impact on age 14 score, namely test score at age 11. We now will include age 11 test score in our model. We should note that adding this variable changes the conceptual nature of our outcome. By evaluating attainment at age 14, after the variance associated with attainment at age 11 has been taken into account, we are effectively evaluating progress between age 11 and age 14. Positive residuals will indicate students making greater than average progress age 11 to age 14, while negative residuals will indicate pupil making less than the average progress between age 11 and 14.

So let’s run Model 6 again, but this time also include age 11 score as a explanatory variable. Additionally, so that we can test whether our interaction terms give a statistically significant increase in r² or not, we will enter the variables in two separate blocks and calculate the r² change, as we did on Page 3.11. First, put ks3stand in the Dependent box. Next add ks2stand, SEChigh, SECmed, SECmiss, gender, and e1-e7 as explanatory variables in Block 1. Finally add all the interaction terms (e.g. e1high, e1med, e1miss, e2high, e2med, e2miss, etc.) as explanatory variables in Block 2. If you want to save the predicted variables they will be called PRE_4 but you do not need them this time so you may prefer to uncheck the unstandardised Predictors box in the SAVE menu.

The figure below shows the model summary (Figure 3.13.1). The r² increase massively from 17.0% in Model 6 up to 79.6% in this model. This testifies to the power of prior attainment as a predictive factor. By knowing how well a student was achieving at age 11, we can explain nearly 80% of the variance in how well they achieve at age 14. It is notable though that the ethnic by SEC interaction terms do not Increase r² significantly. Comparing the main effects model with the interaction model we see that there is no evidence that the inclusion of the interaction terms raises the r² of the model (‘Sig. F Change’, p = .127). The model explains 79.6% of the variance in age 14 scores with or without the interaction effects.

Figure 3.13.1: Model summary when including prior attainment

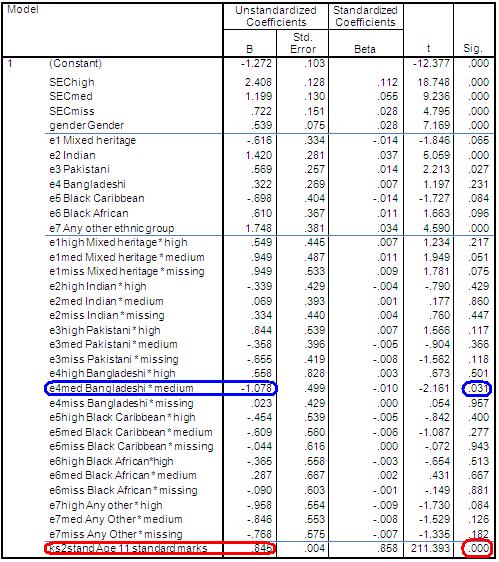
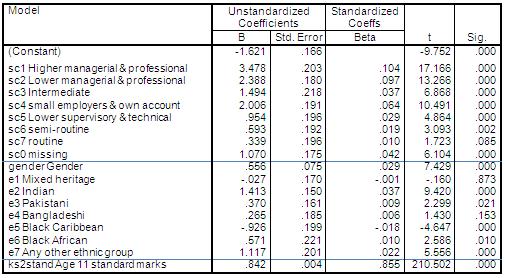
Figure 3.13.2 presents the regression output. While age 11 score is the most powerful explanatory variable in the model (look at the Beta values to get a relative idea) it is not the only significant one. SEC still has a significant association with student progress. White British students from medium SEC homes make 1.2 points greater progress than students of the same prior attainment from low SEC homes, and White British students from high SEC homes make 2.5 points more progress than students with the same age 11 scores from low SEC homes. Gender is also still highly significant, with girls making 0.54 points more progress than boys after control for prior attainment and SEC. Remember that these are effects on student progress. They therefore indicate that social class and gender gaps increase between age 11 and age 14, that is the gaps get wider.

Figure 3.13.2: Coefficients output (Model 7)

Why are the interaction terms no longer significant? The results indicate that some of the ethnic by SEC interactions at age 14 reflect differences in prior attainment at age 11 (not included in earlier models). For example Black Caribbean high SEC students tend to have lower scores at age 11 than White British high SEC students, and this is one reason the age 14 attainment of Black Caribbean high SEC students may have been lower than their White British high SEC peers. Once we take this factor into account the interaction terms are no longer significant. The only exception is Bangladeshi * Medium SEC (p=.031). This may have emerged as statistically significant at the .05 confidence level due to the fact that multiple pairwise comparisons (t-tests) were made. At the .05 level you can expect 1 in 20 pairwise comparisons to emerge as statistically significance by chance alone!

We have arrived at the final model for our regression analysis. HOORAY! Given the interaction terms are not significant, we revert to the eight class SEC variable we used earlier, treated as a set of dummy variables. Our final model (Model 7) is: ks3stand (Dependent), sc0-sc7, gender, e1-e7 and ks2stand.

The r² value of this model is 79.6%, and the coefficients table is presented below.

Figure 3.13.3: Final regression model

The next step is to test the adequacy of the model specification and whether the assumptions of multiple regression analysis, as outlined on Page 3.3, have been successfully met.

Navigation

Home
Modules
Site Guide
Module 3 Contents
Resources