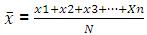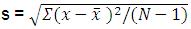1.8 The Normal Distribution
|
We have run through the basics of sampling and how to set up and explore your data in SPSS. We will now discuss something called the normal distribution which, if you haven’t encountered before, is one of the central pillars of statistical analysis. We can only really scratch the surface here so if you want more than a basic introduction or reminder we recommend you check out our Resources
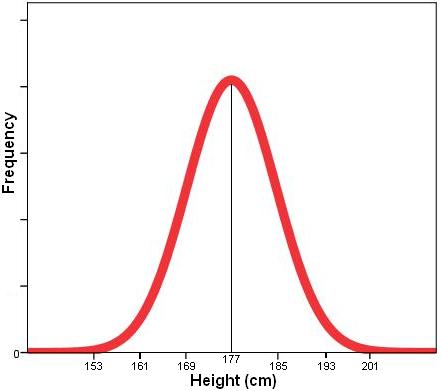
The normal distribution is essentially a frequency distribution curve which is often formed naturally by continuous variables. Height is a good example of a normally distributed variable. The average height of an adult male in the UK is about 1.77 meters. Most men are not this exact height! There are a range of heights but most men are within a certain proximity to this average. There are some very short people and some very tall people but both of these are in the minority at the edges of the range of values. If you were to plot a histogram (see Page 1.5
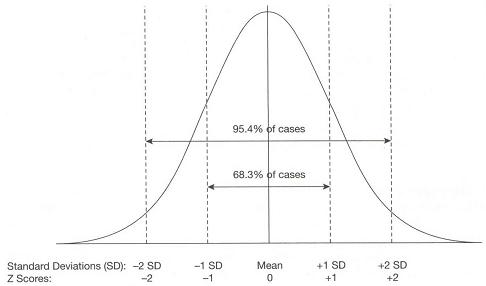
Figure 1.8.1: Example of a normal distribution ‘bell’ curve
Assuming that they are scale and they are measured in a way that allows there to be a full range of values (there are no ceiling or floor effects), a great many variables are naturally distributed in this way. Sometimes ordinal variables can also be normally distributed but only if there are enough categories. The normal distribution has some very useful properties which allow us to make predictions about populations based on samples. We will discuss these properties on this page but first we need to think about ways in which we can describe data using statistical summaries.
It is important that you are comfortable with summarising your variables statistically. If we want a broad overview of a variable we need to know two things about it: 1) The ‘average’ value – this is basically the typical or most likely value. Averages are sometimes known as measures of central tendency. 2) How spread out are the values are. Basically this is the range of values, how far values tend to spread around the average or central point. Measures of central tendencyThe ‘mean’ is the most common measure of central tendency. It is the sum of all cases divided by the number of cases (see formula). You can only really use the Mean for continuous variables though in some cases it is appropriate for ordinal variables. You cannot use the mean for nominal variables such as gender and ethnicity because the numbers assigned to each category are simply codes – they do not have any inherent meaning. Mean: Note: N is the total number of cases, x1 is the first case, x2 the second, etc. all the way up to the final case (or nth case), xn. It is also worth mentioning the ‘median’, which is the middle category of the distribution of a variable. For example, if we have 100 students and we ranked them in order of their age, then the median would be the age of the middle ranked student (position 50, or the 50th percentile). The median is helpful where there are many extreme cases (outliers). For example, you may often here earnings described in relation to the national median. The median is preferred here because the mean can be distorted by a small number of very high earners. Again the median is only really useful for continous variables.
Measures of the spread of valuesOne measure of spread is the range (the difference between the highest and lowest observation). This has its uses but it may be strongly affected by a small number of extreme values (outliers). The inter-quartile range is more robust, and is usually employed in association with the median. This is the range between the 25th and the 75th percentile - the range containing the middle 50% of observations. Perhaps more important for our purposes is the standard deviation, which essentially tells us how widely our values are spread around from the mean. The formula for the standard deviation looks like this (apologies if formulae make you sad/confused/angry): Standard Deviation: Note: The symbol that looks a bit like a capital 'E' means ‘sum of’. This looks more horrible than it is! Essentially all we’re doing is calculating the gap between the mean and the actual observed value for each case and then summarising across cases to get an average. To do this we subtract the mean from each observed value, square it (to remove any negative signs) and add all of these values together to get a total sum of squares. We then divide this by the number of cases -1 (the ‘-1’ is for a somewhat confusing mathematical reason you don’t have to worry about yet) to get the average. This measure is often called the variance, a term you will come across frequently. Finally we take the square root of the whole thing to correct for the fact that we squared all the values earlier. Okay, this may be slightly complex procedurally but the output is just the average (standard) gap (deviation) between the mean and the observed values across the whole sample. Understanding the basis of the standard deviation will help you out later.
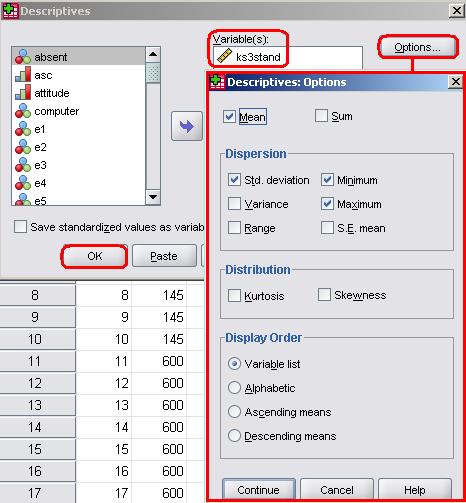
Let’s show you how to get these summary statistics from SPSS using an example from the LSYPE dataset (LSYPE 15,000 To access the descriptive menu take the following path: Analyse > Descriptive Statistics > Descriptives. Move ks3stand from the list of variables on the left into the Variables box. We only need the default statistics but if you look in the Options submenu (click the button the right) you will see that there are a number of statistics available. Simply click OK to produce the relevant statistics (Figure 1.8.2). Figure 1.8.2: Descriptive statistics for age 14 standard marks
Figure 1.8.2 shows that age 14 marks range between -33 and 39 and the mean score is 0. This is because the score has been standardised – transformed in such a way that the mean score is zero and the value for each case represents how far above or below average that individual is (see Extension A
If data is normally distributed, the mean is the most commonly occurring value. The standard deviation indicates the extent to which observations cluster around the mean. Because the normally distributed data takes a particular type of pattern, the relationship between standard deviation and the proportion of participants with a given value for the variable can be calculated. Because of the consistent properties of the normal distribution we know that two-thirds of observations will fall in the range from one standard deviation below the mean to one standard deviation above the mean. For example, for age 14 score (mean=0, SD=10), two-thirds of students will score between -10 and 10. This is very useful as it allows you to calculate the probability that a specific value could occur by chance (more on this on Page 1.9 Figure 1.8.3: Proportion of cases by standard deviation for normally distributed data
These known parameters allow us to perform a number of calculations:
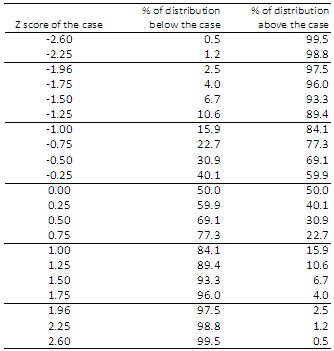
Figure 1.8.4: Table of Z scores
For example, an individual who scores 1.0 SD below the mean will be in the lower 15.9% of scores in the sample. Someone who scores 2.6 SD above the mean will have one of the top 0.5% of scores in the sample. Now that we have seen what the normal distribution is and how it can be related to key descriptive statistics from our data let us move on to discuss how we can use this information to make inferences or predictions about the population using the data from a sample. |