-
- Mod 5 - Ord Reg
- 5.1 Introduction
- 5.2 Ordinal Outcomes
- 5.3 Assumptions
- 5.4 Example 1 - Ordinal Regression on SPSS
- 5.5 Teacher Expectations and Tiering
- 5.6 Example 2 - Ordinal Regression for Tiering
- 5.7 Example 3 - Interaction Effects
- 5.8 Example 4 - Including Prior Attainment
- 5.9 Proportional Odds Assumption
- 5.10 Reporting the Results
- 5.11 Conclusions
- 5.12 Other Categorical Models
- Quiz
- Exercise
- References
- Mod 5 - Ord Reg

5.6 Example 2 - Running an Ordinal Regression for Mathematics Tier of Entry
|
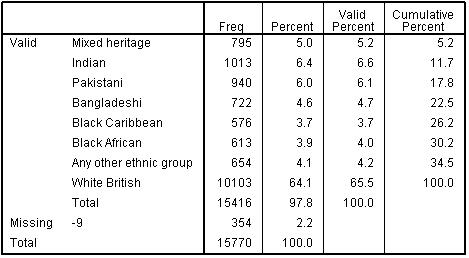
Remember that we said that SPSS ordinal would automatically make the reference category for a nominal explanatory variable the last category. We want the reference group for ethnicity to be White British as this is the majority ethnic group, but White British students are currently coded 0 in the variable ethnic. We therefore need to RECODE (we discuss recoding variables in the Foundation Module Figure 5.6.1: Frequency Table for recoded Ethnicity Variable
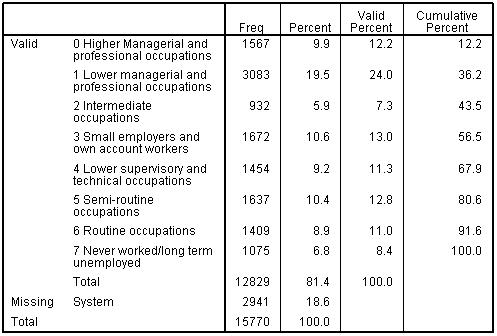
We are also going to take advantage of the fine-grained hierarchical nature of the SEC variable to treat this as a continuous variable. It is helpful in all forms of regression if the zero value of a continuous explanatory variable (or covariate) has an interpretable meaning, and this is particularly the case in logistic and ordinal regression. We have therefore recoded SEC so zero is a meaningful category (the highest level of SEC, higher managerial and professional homes) and have called this recoded variable Sec2. (If you are unsure how to do this we explain the process in the text surrounding Figure 5.7.4) The frequencies for Sec2 are displayed in Figure 5.6.2. Figure 5.6.2: Frequency Table for recoded SEC Variable
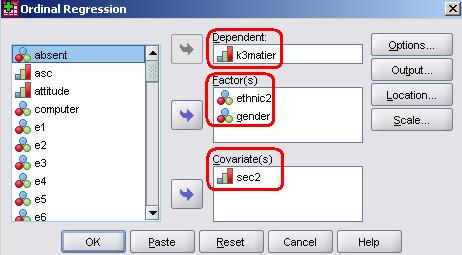
We request an ordinal regression as we did earlier, through Analyse > Regression > Ordinal. We enter k3matier as our Dependent variable. Categorical (nominal or ordinal) explanatory variables are entered to the Factor(s) box, so this is where we enter ethnic2 and gender. Continuous explanatory variables (in this case sec2) are entered as covariates.
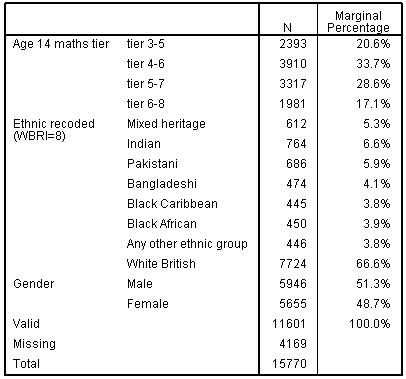
The case processing summary is a reminder of the variables we have entered (Figure 5.6.3), note though that it does not display any covariates in the model. Note that SPSS also issues a warning that there are “20 (3.9%) cells with zero frequencies”. This just means that even with 11,601 cases there are some combinations of variables that are not represented (for example there are no Bangladeshi, boys, from higher managerial and professional homes entered for the bottom tier). This does not mean we cannot complete an analysis; there may be sound empirical reasons for low counts in some cells. However we should consider the proportion of empty cells when we come to evaluating the goodness-of-fit test.
Figure 5.6.3: Case Processing Summary
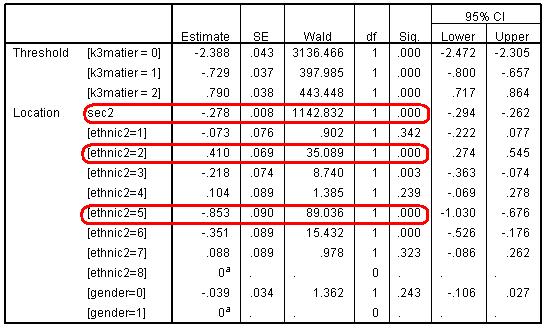
Let’s look at the Parameter Estimates table (Figure 5.6.4). The model confirms there are systematic effects in tier of entry related to SEC and to ethnic group. In relation to Sec2 the coefficient is -.278. We take the exponent of this coefficient to get the OR: exp(-.278)=.78, which indicates that odds of being entered for a higher tier decrease by 0.78 for each unit increase in Sec2 score (remember higher values of SEC indicate lower SEC homes). Conversely we could say the odds of being entered to a higher tier increase by (1/0.78)=1.33 for ever unit change in Sec2 score. To calculate the predicted OR at any point on the SEC scale we can multiply the coefficient by the relevant Sec2 score and take the exponent of the result. For example the OR for students from the lowest social class category (7=long term unemployed) is exp(-0.78 * 7) = 0.143. Students from homes where the main parent is long term unemployed are only .14 as likely to be entered for a higher tier compared to the odds for a student from the higher managerial and professional home. To express this as the OR in favour of high SEC (1/.143=7.00) indicating students from the highest SEC are 7 times more likely than students from the lowest SEC to be entered for a higher tier. Figure 5.6.4: Parameter Estimates for the Model There is also a strong association between ethnic group and tier entry, even after SEC has been controlled. We can see significant and negative coefficients for Black Caribbean, Black African and Pakistani students. Again taking the exponent of the logits will give the OR, so for example the odds of Black Caribbean (ethnic=5) students being entered for a higher tier are exp(-.853)= 0.43 the odds for White British students, or less than half. Conversely there is a significant positive coefficient for Indian students (.410) indicating they are exp(.410)=1.51 times more likely than White British students to be entered for a higher tier, even after controlling for SEC.
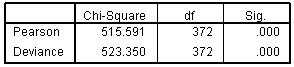
Of course we should not take the above at face value without examining the adequacy of the model and particularly the proportional odds assumption. Looking at the model fit (Figure 5.6.5) we can see a highly significant reduction in the chi-square statistics (p<.005) so the model is clearly a significant improvement over the baseline or intercept only model. The Nagelkerke R2 indicates the model can account for 12.4% of the variance in tier of entry. Figure 5.6.5: Model-fit Data However the goodness-of-fit statistics (Figure 5.6.6) suggest the model does not fit the data well. Figure 5.6.6: Goodness of Fit for Model And the test of parallel lines (Figure 5.6.7) also rejects the null hypothesis of the assumption of PO. Figure 5.6.7: Test of Parallel Lines These statistics suggest the model does not fit the data well. We said earlier that these statistics can be unreliable in certain circumstances. For example the large sample size here means that even very small departures from the PO assumption may be found to be statistically significant. We will explore what to do in these circumstances in more detail later (Page 5.9 |