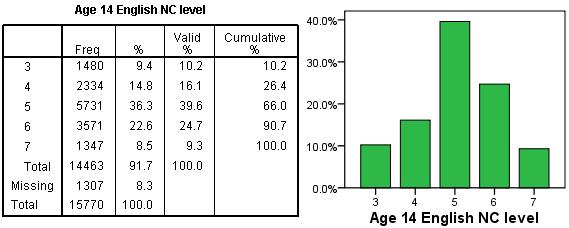
In previous modules we have seen how we can use linear regression to model a continuous outcome measure (like age 14 test score), and also logistic regression to model a binary outcome (like achieving 5+ GCSE A*-C passes). However you will remember from the Foundation Module that we typically define measures at three levels: nominal, ordinal and continuous. What we have not covered therefore is this ‘intermediate’ level where our outcome is ordinal. You will remember that an ordinal measure includes information on rank ordering within the data. For example we might have Likert scale measures such as “How strongly do you agree that you love statistics” which may be rated on a 5 point scale ranging from strongly disagree (1) to strongly agree (5). Another example is OFSTED (Office for Standards in Education) lesson evaluations which may be graded as ‘unsatisfactory’, ‘satisfactory’, ‘good’ or ‘outstanding’. Such examples are common in the social sciences.

There are a number of ordinal outcomes in our LSYPE dataset. One is the KS3 (age 14) English test level. In England students’ performance is recorded in terms of national curriculum (NC) levels. These levels are reported on an age related scale, with the ‘typical’ student at age 7 expected to achieve level 2, at age 9 level 3, at age 11 level 4, and at age 14 somewhere between level 5 and level 6. These levels may be determined through teacher assessment or be expressed as summaries from continuous test marks. Figure 5.1.1 shows the distribution of students by English level from our dataset.

Figure 5.1.1 Proportion of students at each English test level

We do have access to the actual test marks in LSYPE, but often test marks are not available and NC levels might be the only data recorded. In any event, this is a good example of an ordinal outcome which we can work with to demonstrate the particular analyses that you can apply when your outcome measure is ordinal.

The good news is that, bar a little extra work, the assumptions and concepts we need for ordinal regression have been dealt with in the Logistic Regression Module (Phew!). The key concepts of odds, log-odds (logits), probabilities and so on are common to both analyses. It is absolutely vital therefore that you do not undertake this module until you have completed the logistic regression module, otherwise you will come unstuck. This module assumes that you have already completed Module 4 and are familiar with undertaking and interpreting logistic regression.

Navigation

Home
Modules
Site Guide
Module 5 Contents
Resources