Overview

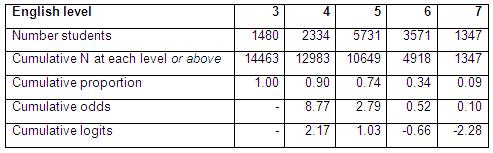
What do we mean by the assumption of proportional odds (PO)? To explain this we need to think about the cumulative odds. Figure 5.3.1 takes the data from Figure 5.1.1 to show the number of students at each NC English level, the cumulative number of students achieving each level or above and the cumulative proportion. Remember proportions are just the % divided by 100. We can see that the proportion achieving level 7 is 0.09 (or 9%), the proportion achieving level 6 or above is 0.34 (34%) and so on.

From this we can calculate the cumulative odds of achieving each level or above (if you require a reminder on odds and exponents why not check out Page 4.2?). 1,347 students achieved level 7 compared to 13,116 who achieved level 6 or below. Therefore the odds of achieving level 7 are 1,347/13,116 = 0.10. Similarly the odds of being at level 6 or above are 4918 / 9545 = .52. The odds of achieving level 6 or above are about half that of achieving level 5 or below. If you are getting confused about the difference between odds and proportions remember that odds can be calculated directly from proportions by the formula p / (1-p). Therefore the cumulative odds of achieving level 7 are .09 / (1-.09) = 0.10. Similarly the cumulative odds of achieving level 6 or above are .34 / (1-0.34) =.52. We can do the same to find the cumulative odds of achieving level 5 or above (2.79) and level 4 or above (8.77). We do not need to calculate the cumulative odds for level 3 or above since this includes the whole sample, i.e. the cumulative proportion is 1 (or 100%). As you can see we have essentially divided our ordinal outcome variable in to four thresholds.

Table 5.3.1: Cumulative odds for English level

In the table we have also shown the cumulative log-odds (logits), this is just the natural log of the cumulative odds which you can calculate in EXCEL or on a scientific calculator. Log odds rather than odds are used in ordinal regression for the same reason as in logistic regression (i.e. they do not suffer from the ceiling and floor effects that odds do, you should remember this from Module 4).

The key assumption in ordinal regression is that the effects of any explanatory variables are consistent or proportional across the different thresholds, hence this is usually termed the assumption of proportional odds (SPSS calls this the assumption of parallel lines but it’s the same thing). This assumes that the explanatory variables have the same effect on the odds regardless of the threshold. For example if a set of separate binary logistic regressions were fitted to the data, a common odds ratio for an explanatory variable would be observed across all the regressions. In ordinal regression there will be separate intercept terms at each threshold, but a single odds ratio (OR) for the effect of each explanatory variable. This is best explained by an example.

As example using gender and English NC level

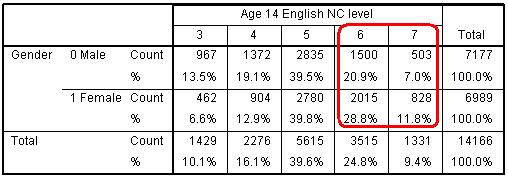
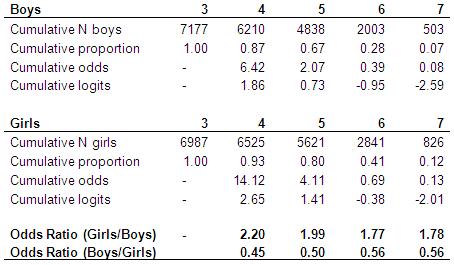
As a simple example let’s start by just considering gender as an explanatory variable. Before you start building your model you should always examine your ‘raw’ data. Figure 5.3.2 shows the cross tabulation of English level by gender.

Figure 5.3.2: Gender by English level crosstabulation

Clearly girls tend to achieve higher outcome levels in English than boys. What does this look like in terms of the cumulative proportions and cumulative odds? In Figure 5.3.3 we calculate the cumulative odds separately for boys and for girls.

Figure 5.3.3: Cumulative odds for English NC level separately for boys and girls

We can calculate odds ratios by dividing the odds for girls by the odds for boys. In general the odds for girls are always higher than the odds for boys, as proportionately more girls achieve the higher levels than do boys. These odds ratios do vary slightly at the different category thresholds, but if these ratios do not differ significantly then we can summarise the relationship between gender and English level in a single odds ratio and therefore justify the use of an ordinal (proportional odds) regression. If we do calculate the odds ratio from an ordinal regression model (as we will do below) this gives us an OR of 0.53 (boys/girls) or equivalently 1.88 (girls/boys), which is not far from the average across the four thresholds. This assumes the odds for girls of achieving level 4+ are 1.88 greater than the odds for boys; the odds of girls achieving level 5+ are 1.88 times greater than the odds for boys, and so on for level 6+ and level 7... i.e. that the odds of success for girls are almost twice the odds of success for boys, wherever you split the cumulative distribution (that is to say, whatever threshold you are considering). SPSS has a statistical test to evaluate the plausibility of this assumption, which we discuss on the next page (Page 5.4).

Navigation

Home
Modules
Site Guide
Module 5 Contents
Resources