There are three general ways we can approach modelling of an ordinal outcome:

A) Treat the outcome as a continuous variable

You may look at Figure 5.1.1 and ask why you cannot treat this as a continuous variable and use linear regression analysis. After all, there are a reasonable range of categories (five), with a fair spread of observations over all the categories and an approximately normal distribution. While this may not be unreasonable in this particular case, it does mean making assumptions about continuity in the data which are not strictly verifiable, and of course a mean level is not what we want to predict when our outcome is strictly ordinal (for example a student cannot achieve level 3.75 or level 4.63 in the National Curriculum in England - levels can only be awarded as whole numbers; 4, 5, 6 etc.). There are many other cases and examples where the linear assumption will not hold, where there are fewer than five categories or an uneven distribution across categories, or it is unreasonable to suppose an underlying continuous distribution. In such cases the choice of ordinal regression may be even clearer!

B) Treat the outcome as a series of binary logistic equations

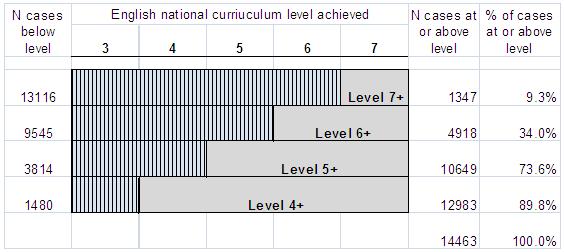
We could treat the analysis as a series of logistic regressions by splitting or cutting the distribution at key points. This is illustrated in Figure 5.2.1.

Figure 5.2.1: Four different ways to split the English NC level outcome

For example, we may consider comparing those students who have achieved level 7 versus those who have not using a logistic regression. We might want to ask whether girls were more likely to achieve this level of success than boys, or whether there are ethnic or social class differences in the probability of achieving level 7. We can do the same thing for those who achieve level 6 or above, compared to those who achieve below level 6. Again this is a binary logistic regression, splitting the sample into two, only this time in a different place. The same can be done to compare the probability of achieving level 5 or above, and again for the probability of achieving level 4 or above. In each case we complete a binary logistic regression to evaluate the effect of our explanatory variables on the likelihood of success at different thresholds (level 4+, level 5+, level 6+ and level 7). Note we do not need a category for level 3+ because this includes all (100%) of the cases in our data.

Essentially we have turned our outcome into a series of binary measures reflecting the cumulative outcomes at different thresholds. However estimating four separate binary logistic regression equations is wasteful of the information on ordinality in our outcome and may lead to estimating more parameters than are necessary to account for the relationships between our explanatory variables and the outcome (four sets of estimated regression coefficients rather than one set). What we want ideally is a single model of the effect of our explanatory variables on the outcome which utilises the ordinality present in the outcome variable.

C) Model the ordinality in the outcome

In ordinal regression instead of modelling the probability of an individual event, as we do in logistic regression, we are considering the probability of that event and all others above it in the ordinal ranking. We are concerned with cumulative probabilities rather than probabilities for discrete categories. If a single model could be used to estimate the odds of being at or above a given threshold across all cumulative splits, the model would offer far greater parsimony compared to fitting multiple (in the case of our English level example, four) separate logistic regression models corresponding to the sequential splits in the distribution as illustrated above. The goal of such a cumulative odds model is to simultaneously consider the effects of a set of explanatory variables across these possible consecutive cumulative splits in the outcome. To do this we make the simplifying assumption that the effects of our explanatory variables are the same across the different thresholds, the assumption of proportional odds. If this assumption is met there is much to gain from a single parsimonious model, as we shall see. Let us now look at this important assumption of proportional odds in more detail.

Navigation

Home
Modules
Site Guide
Module 5 Contents
Resources