|
|
|
|
|
|
|
>2.1 Background >2.2 Getting started > 2.3
Results for simple tabulations
>2.4 Chi squared tests > 2.5 Results for sub groups >2.6 Results for logistic modelling
> 2.7 Data problems > 2.8
Details of the survey > 2.9 Details of the
dataset
|
|
|
 top
This exemplar is about using data from the Scottish Household Survey (SHousS) to
look at factors determining internet use by Scottish adults.
It uses interviews carried out in 2001/2002 with data from
the "Random Adult" data set from this survey. There were 28
685 respondents in these two years. To find out how data were
prepared for analysis click here. To
prevent identification of individuals we have modified the
data and taken other precautions as described here.
The analyses examine factors that determine which adults in
Scotland use the internet and, in particular,
- differences between geographic areas in internet
use
- modelling internet use by age and sex of the adult and
other factors
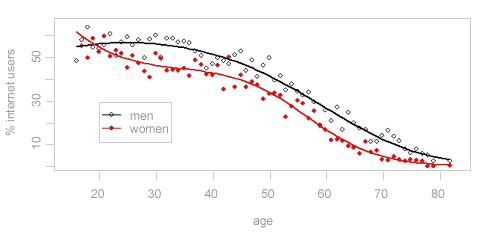
Fig 1.1 Internet use by age and gender 2001/02.
This figure was plotted from
a logistic regression model fitted with a procedure for
survey data. The dots are the data for each age sex group and
the lines are the model fit. Both the data and the fit are
adjusted for survey weights. The R
package was used to make this plot.
|
Links to explanation and theory
|
Details for this
survey
|
Special aspects
|
|
|
click here |
Design weights and  post-stratification to local
authoriy totals post-stratification to local
authoriy totals
|
|
|
click here |
Clustered only in rural areas |
|
|
click here |
Larger sampling fractions in small
local authorities
|
|
|
click here |
 design
effects and design
effects and  design
factors can be very different for subgroups
compared to those for the whole survey. design
factors can be very different for subgroups
compared to those for the whole survey.
|
|
|
|
Different sized tables. |
|
|
click here |
Small inconsistencies between the
design and the data, often involving only a few
respondents can cause severe analysis problems unless
you know how to look out for them and handle
them.
|
Table 2.1 Features illustrated
in this exemplar
This survey has a fairly
complicated design, and weighting structure. It can be
handled by any of the packages used here, but it needs to be
set up with care.
|
|
 The code to produce
this plot in R can be viewed here. The code to produce
this plot in R can be viewed here.
|
|
|
|
|
 top
From links in this section you can:-
- Downlaod or open the data
files
- Analyze them with any of the
4 packages you have available
- View the code (with
comments) and the ouput, even if you don't have
the software.
To start, click the mini guide for the statistical
package you want to use to analyse Exemplar 2.
For additional help click on the appropriate
novice guide.
For details of the data set see below.
|
|
|
Table 2.2 Data sets
and code.
|
* SAVE these files to your computer They do not
open from outside the software packages.
You may have to save some of the other files to
disc if your set-up does not allow you to open files
directly.
The html files allow you to view program code and
results outside packages.
|
|
|
� |
|
|
|
|
 top
We look at the proportion of random adults who have access
to the internet and then at the proportions who spend
different numbers of hours per week on the internet.
The weighted percentage for internet using adults was 34%,
compared with the unweighted percentage of 31%. This
difference reflects the fact that people who live alone (and
are thus relatively downweighted in the survey) are older and
less likely to be internet users.
We can calculate the percentage internet
use by men and women separately. All the packages agreed on
the answers for proportions, their  design factors
and design factors
and  confidence
intervals . The proportions also agreed with the
results in Chapter 6 of the report of the SHousS. Because of
the large numbers the confidence intervals are fairly
narrow. confidence
intervals . The proportions also agreed with the
results in Chapter 6 of the report of the SHousS. Because of
the large numbers the confidence intervals are fairly
narrow.
The results below were taken from Stata, but other programs
gave very similiar results
| � |
� |
Percentage |
Std error |
Design effect |
95% Confidence Interval |
|
Internet Use
intuse= 0
intuse= 1
|
no
yes
|
65.8%
34.2%
|
0.34%
0.34%
|
1.48
1.48
|
65.2% - 66.5%
33.5% - 34.8%
|
|
Hours per week
RC5=1
RC5=2
RC5=3
RC5=4
RC5=5
|
under 1
1-5 hrs
5-10 hrs
10-20 hrs
20 + hrs
|
40.9 %
40.5 %
10.9 %
5.1 %
2.6 %
|
0.60%
0.60%
0.38%
0.27%
0.19%
|
1.36
1.33
1.30
1.38
1.34
|
39.7% - 42.1%
39.4% - 41.7%
10.1% - 11.6%
4.5% - 5.6%
2.2% - 3.0%
|
|
Bases 28 685 respondents of whom 8 862 used
internet
|
Internet use
by sex
|
� |
Percentage
|
Std error
|
Design effect
|
95% Confidence Interval
|
|
intuse=1
intuse=1
|
men
women
|
38.5%
30.7%
|
0.51%
0.43%
|
1.41
1.41
|
37.5 - 39.5%
29.8 - 31.6%
|
|
Bases 12 174 (men) 16 511 (women)
|
Table 2.3 Internet use hours
per week
We can readily test this out by analysing the data as if it
were from another design. The estimate of internet use is the
same for all cases as the weights do not change. To find out
more about clustering click here.
|
Design
|
Standard Error |
Design Effect (DE) |
| Weighted sample but no
clustering or statification
|
0.33%
|
1.36
|
| Weighted sample with
clustering
|
0.38%
|
1.81
|
| Weighted sample with
stratification no clustering
|
0.32%
|
1.27
|
| Weighted sample with
clustering and stratification
|
0.37%
|
1.48
|
Table 2.4 The effect of design
factors on the precision of estimation of % of internet
use
We can see that there is a substantial design effect due
to unequal sampling fractions (line 1). This is made worse by
clustering (line 2), improved by stratification (line 3) and
allowing for the full design (line 4) gives a DE of 1.48.
Note The design effect of 1.48 for the
effect of all the design aspects on this measure is different
from the design effect of 1.04 (the quoted design factor of
1.02 squared) quoted in the technical report for this variable. This
is being discussed with the survey contractors.
The large increase in the DE due to clustering seems, at
first sight, a bit surprising here. Only a part of the sample
used cluster sampling (60%, weighted data). But the use of
relatively small units (Enumeration Districts) may have had
the effect of making them very homogeneous for something like
internet use which may be heavily clustered by geography.
|
|
 Click these links
to open small windows giving the code to get these results in Click these links
to open small windows giving the code to get these results in
Stata, R, SPSS and SAS.
and these links to see the output
produced by each package Stata, R, SPSS SAS.
 Click these links
to open small windows giving the code to compare these design effects
in Stata, R, SPSS. Click these links
to open small windows giving the code to compare these design effects
in Stata, R, SPSS.
SAS does not calculate design effects
but the output file has been annotated to show you how to calculate
them, click here and follow links to check this SAS.
and these links to see the output
produced by each package Stata, R, SPSS and SAS.
|
|
|
|
|
 top
To investigate differences between groups, such as
differences in internet use between men and women a
chi-squared test would be the normal procedure.
But the ordinary formula for a chi-squared test needs to
be modified to allow for the design of the survey more about chi squared tests.
Here are the results obtained for a weighted table of
internet use by gender.
| sex
|
Percentage adults using the internet
|
|
no
|
yes
|
Total
|
Base
|
male
female
Total
|
|
38.51
30.70
34.15
|
100
100
100
|
12 174
16 511
28 685
|
Tests of association
Uncorrected chi2(1) = 191.89
Design-Based (null) F(1,
11833) = 143.81 P = 0.0000 |
Table 2.5 Internet use by gender with
adjusted chi-squared test
Results here, from Stata, give the and the commonest adjusted test which
is expressed as an F statistic. The uncorrected chi-squared
value here is the value for the weighted table. It would not
have a chi-squared distribution if there were no association
in the table, because of the weighting and other features of
the design. The adjusted test shown here is an F test. Since
there is only 1 degree of freedom here the chi-square and F
tests are directly comparable. Other packages produce similar
results based on slightly different adjusted tests.
Obviously, we did not need either test to show that there
was overwhelming evidence that men used the internet more
than women. Things are not quite so clear when we investigate
the proportion of adults who use the internet for grocery
shopping (variable RC7E recoded to GROC so that non-internet
users are coded as 'no')). Is this the one area of internet
use where women are more frequent users than men? The
chi-squared test shows that although women's percentage in
the table is higher, this could just be a chance finding.
| sex
|
% using in
ternet for groceries
|
|
no
|
yes
|
Total
|
male
female
Total
|
97.28
97.03
97.14
|
2.723
2.967
2.86
|
100
100
100
|
Tests of association
Pearson: Uncorrected chi2(1) = 1.4349
Design-based F(1, 11833)
= 1.0726 P = 0.3004 |
Table 2.6 Internet grocery
shopping by Stata output with adjusted chi-squared test
Chi-squared (X2) tests for larger tables can be
used to screen variables for evidence of an association. In
the table below there appears to be an association, for
internet users, between employment status and the time spent
on the internet per week. Presentation here follows
recommendations for weighted tables. But
some of the bases are rather small, so perhaps some of the
associations are just chance.
|
|
up to 1 hr per
week
|
over 1 hour up to 5 hours
|
over 5 hours up to 10 hrs
|
over 10 hours up to 20 hrs
|
over 20 hours
|
all
|
base
|
|
Self employed
|
40
|
41
|
10
|
6
|
2
|
100
|
647
|
|
Employed full time
|
41
|
42
|
10
|
5
|
2
|
100
|
4743
|
|
Employed part time
|
52
|
35
|
8
|
3
|
2
|
100
|
1029
|
|
Looking after the
home and family
|
45
|
39
|
9
|
3
|
3
|
100
|
490
|
|
Permanently retired
|
50
|
36
|
10
|
2
|
1
|
100
|
668
|
|
Seeking work
|
34
|
38
|
16
|
7
|
5
|
100
|
232
|
|
At school
|
37
|
36
|
12
|
11
|
4
|
100
|
159
|
|
In higher education
|
23
|
46
|
18
|
8
|
5
|
100
|
603
|
|
Govt work/training
|
26
|
31
|
10
|
18
|
15
|
100
|
11
|
|
Sick/disabled
|
41
|
29
|
10
|
9
|
11
|
100
|
187
|
|
unable to work -
illness/long term injury
|
39
|
27
|
14
|
7
|
13
|
100
|
52
|
|
Other
|
27
|
36
|
22
|
3
|
12
|
100
|
50
|
| F = 7.191, ndf = 42.015, ddf =
205243.504, p-value < 2.2e-16 |
Table 2.7 Time spent using
internet each week by employment status (internet users only)
row percentages.
Here the design-based test is based on an
F-test with approximately 42 degrees of freedom in the
numerator and a very large number of degrees of freedom in
the denominator. Clearly there are very strong associations
to investigate further here. Almost all the tests in this
section have shown very powerful associations. This is
largely due to the large size of the sample which shows up
small differences very clearly, even when they are too small
to be important.
|
|
 Click these links
to open small windows to show how to carry out these and other chi
squared tests in Stata, R, SPSS. Click these links
to open small windows to show how to carry out these and other chi
squared tests in Stata, R, SPSS.
SAS 8 doesn't do chi squared tests for weighted tables, but it does
allow you to get good table layouts. For code click SAS.
and these links to see the output
produced by each package Stata, R, SPSS and SAS.
|
|
|
|
|
 top
Survey analyses of subgroups can be done in two ways:
1. Subdivide the data and then define the survey
2. Set up the survey and request the analysis of a
subgroup
The first one is usually wrong for a stratified sample as
it would assume the subgroup was stratified, which was not
the case.
But there is an exception when a survey has all its design
features (startification, clustering,  post-stratification ) carried out
within sub-groups. This was true for the SHousS for local
authority areas and subsets of the data by local authority
can be analysed as if they were independent surveys. post-stratification ) carried out
within sub-groups. This was true for the SHousS for local
authority areas and subsets of the data by local authority
can be analysed as if they were independent surveys.
For subgroups that were not designed in this way it is
essential to use method 2. Design effects for subgroups that
select members from different clusters and strata tend to
have design effects closer to 1 than the analyses for the
whole survey. The theory section on subgroups explains this in more
detail. An example for this survey is in the results by
gender in Table 2.3 above although the effect is very modest
here. The P|E|A|S code always uses method 2, and exemplar 1
illustrates how design effects for a subgroup can be very
different to those for the whole survey. (NOTE ADD LINK HERE)
The SHS was designed to be large enough to
give results with good precision at the local authority (LA)
level. The design was stratified
and  post-stratification post-stratification within each LA.
We can see that internet use varies sharply by local
authority and that the aim of the survey, is to get estimates
of similar precision by LA , has been met.
 |
| LA
|
% use |
s.e. |
Design Effect |
Aberdeen
Aberdeenshire
Angus
Argyll_&_Clyde
Clackmannan
Dumfries & G
Dundee
East Ayrshire
East_Dunbart
East_Loth
East_Renf
Edinburgh
Eilean_Siar
Falkirk
Fife
Glasgow
Highland
Inverclyde
Midlothian
Moray
North_Ayr
North_La
Orkney
Perth_&_K
Renfrewshire
Borders
Shetland
South_Ayr
South_Lanark
Stirling
West_Dunbart
West_Lothian
|
43
37
36
33
30
25
31
30
47
38
44
45
26
34
33
28
38
30
35
31
25
28
31
38
32
36
47
33
32
43
28
35
|
2
2
3
3
3
2
2
3
2
3
2
1
2
3
2
1
2
2
3
3
2
2
3
2
2
3
3
3
2
3
2
3
|
1.15
1.53
1.38
1.84
2.28
1.16
1.22
1.61
1.26
1.64
1.19
1.17
1.37
1.29
1.52
1.22
1.32
1.26
1.46
1.76
1.92
1.72 2.72
1.48
1.27
1.94
2.05
1.95
1.73
1.65
1.40
1.43
|
|
Figure 2.2 Internet use by LA
We can use the width of confidence intervals to indicate when
there is evidence of a difference by LAs. The design effects
presented above were calculated by Stata.
There are two different ways we can specify design effects
for sub-populations.
1) The presented here is an option in Stata and the default
method used in R gives the design effect for taking a random
sample from the subpopulation that is the same size as those
in the sample. So if we were to the data to interviews in
Orkney we get exactly the same estimate and confidence
interval but a Design Effect of 2.7. This shows the price we
are paying for a clustered design in a rural area.
2) The alternative which is the default Stata option
calculates the DE with respect to a random sample of all
households for the whole of Scotland. This gives a very small
design effect for Orkney and Shetland because these areas
were heavily over-sampled. A random sample for all of
Scotland would give many fewer interviews to the islands.
|
|
 Click these links
to open small windows to show how to carry out analyses of subgroups
for this survey in Stata, R, SPSS and SAS. Click these links
to open small windows to show how to carry out analyses of subgroups
for this survey in Stata, R, SPSS and SAS.
and these links to see the output
produced by each package Stata, R, SPSS and SAS.
|
|
|
|
|
From the tables above it is clear that there are many
factors influencing internet use. A multivariate analysis
should shed some light on this. Since internet use is a
binary variable, we need a logistic regression model (or
something similar). Only R and Stata currently offer this for
surveys.
The modelling process is typically long, and we illustrate
only a small part of it for each package.
In Stata the analysis looks at the joint impact of
household income and urban/rural classification on Internet
use. Fitting grouped income first we get the table of odds
ratios below for two methods of analysis.
| Survey logisitic regression
|
Simple logistic regression
|
|
| intuse |
Odds Ratio
|
Std. Error
|
t
|
intuse |
� Odds Ratio |
Std Error |
t
|
<10K(base)
��10-20K
��20-30K
��30-50K
��50K +
|
1 (base)
2.06
5.22
13.08
22.63
|
-
0.09
0.25
0.75
2.86
|
-
16.29
35.07
44.63
24.65
|
<10K(base)
��10-20K
��20-30K
��30-50K
��50K +
|
1 (base)
2.55
6.62
15.67
26.54
|
-
0.10
0.27 0.80
2.92
|
-
24.3
45.8
54.1
29.8
|
Table 2.8 Logistic regression
to predict internet use from income.
We see a very steep increase
in odds with income, but standard errors that are somewhat
smaller in the simple, inappropriate regression. Adding the
urban rural classification into this model adds relatively
little with the large urban areas and the most remote areas
having higher internet use than other areas. But the effect
is small compared to income. The results files for Stata and
R give the details.
|
|
 Click these links
to open small windows to show how to carry these logistic regressions
in Stata, R, Click these links
to open small windows to show how to carry these logistic regressions
in Stata, R,
and these links to see the output
produced by each package Stata, R,
Logistic regression is not available in SPSS 12 or SAS 8, but it is
in later versions.
|
|
|
|
|
 top
Survey design analyses require the data to agree with the
sampling design. Problems arose
with the data for this exemplar because
1. Two
 PSUs PSUss
had addresses that were in two different local authorities
2. Some of the strata included only one PSU.
This was mainly because the PSU identifiers were not supplied
with the data file sent to the data archive and so had been
little tested. They were obtained from the survey contractors
directly. There were several interviews with missing or wrong
Mosaic codes. Also, a few less common Mosaic codes had only
one interview in a local authority (e.g. remote rural in a
largely urban LA).
A lot of programming was needed to fix this.
If the data breaks any of these rules then the programs
may do various things, as shown below.
| Problem |
SAS |
Stata |
R |
SPSS Survey |
Clusters that
split across~
strata
|
Splits clusters
to make
new strata
|
Splits clusters
to make new
strata
|
Fails but
setting options
can allow recovery
|
ignores problem |
strata
with just
one primary
sampling unit
|
Sets variance
in this stratum
to zero
|
Fails |
Fails but
options
can allow
various
choices
|
ignores problem |
Table 2.9 How packages handle
data that does not conform to the design.
To overcome these problems the data sets for this exemplar
have been corrected by:
- Re-assigning local authority codes in the two PSUs
- Pooling strata with only one PSU
What happens when a variable has missing values so that a
few strata may be reduced to only one PSU?
The same problems can arise, again Stata fails.
The original data, without these corrections,
is available to allow you to investigate how these problems
might be handled by different packages.
|
Package
|
Uncorrected data sets
|
Program
code
|
Output
|
|
SAS
|
|
|
|
|
Stata
|
|
|
|
|
SPSS
|
|
|
|
|
R
|
|
|
|
Table 2.10 Analyses with
uncorrected data
|
|
� |
|
|
|
|
 top
A comprehensive description of the design of the survey
can be found in the Technical Report for the 2001/02 surveys,
Scotland's People; Volume 8 on which the
summary below is based.
The sampling frame is the post code address file a list from the
post office of all addresses in the UK. We are using data
from the two years 2001 and 2002. The data set includes
28,685 records of interviews with random adults.
A simple random sample of households was selected in local
authorities (LA's.) with densities of 500 or more people per
sq km. For the remaining LAs a cluster sample was selected
with the enumeration district (ED's) as the PSU. These are
fairly small areas that represent one census enumerator's
work load. The survey aimed to achieve 11 interviews per PSU.
The sampling fractions varied by LA, with larger sampling
fractions in the smaller LAs in order to assure a sample size
of 500 households in each LA over a two year period.
The SHS sample was first stratified by LA and then by 10
mosaic categories within each local authority.
Mosaic is a socio-economic clasifiaction
applied at the post code level. For areas with cluster
sampling stratification was the commonest mosaic code in the
ED was used. The stratification was explicit at the first
stage and then implicit, by ordering the units, within each
LA. The theory section describes implicit
and explicit stratification. The strata in the file are
labelled by a combination of Mosaic code and LA. Some strata
can contain only a small number of units. If, perhaps due to
the selection of subgroups, we
are left with only one unit in a stratum problems can arise,
as discussed in the section on data
checking above. The main data set provided here has the
strata merged to avoid these problems.
One adult was selected at random per household. This means
that people from larger households have less chance of being
selected than those in smaller households. To adjust for this
a weight is applied to the random adult data that is
proportional to the number of adults in the household. This
for households with 1,2,3,4,.,. adults the weights are
proportional to 1,2,3,4,.,.
The two largest factors contributing to the weights for the
random adult data (IND_WT) are the unequal fractions by local
authority and the selection of just one adult per household.
Additional weighting is carried out compensate for
differential non-response by LA. These final weights make the
weighted survey totals of 'random adults' match the 2001
census population in private households. This adjustment is
minor compared to the others. No further weighting is carried
out to make the sample match the populations by age and sex.
The justification for this, along
with a discussion of the representativeness of the
sample can be found in the Technical Report, Scotland's People; Volume 8 The
weights span a fairly wide range, from 0.07 to 6.2 as
is illustrated in the histogram on the
right.
|
����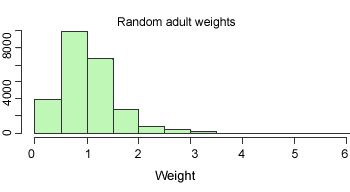
Fig. 2.3 Random adult weights
|
|
|
� |
|
|
|
|
 top
We have constructed a data set for this analysis with just
those variables we will use in these analyses. The process by
which the data set has been constructed and the programmes
used to make it from data that is available from the Essex Data Archive are explained in
detail for anyone who has an interest in this. The variable
to identify the  PSUs
is not available from the archive, but was provided
to us directly by the SHousS team. PSUs
is not available from the archive, but was provided
to us directly by the SHousS team.
Several procedures to anoymise the data have been carried
out along the lines described here.
This means that the answers obtained from analysing this data
set may be very slightly diferent from what would be obtained
from the archive data. The variables in the data files
are:
| Name
|
Variables |
Formats
|
| UNIQD
|
Unique household identifier |
scrambled for
anomymity
|
| COUNCIL
|
code for Scottish local
authority
|
see
codebook |
| INTUSE
|
whether uses internet |
1=yes 0
=no
|
| SHS_6CLA
|
six fold regional
classification
|
see
codebook |
| RC5
|
number of hours of internet
p/w
|
see
codebook |
| AGE
|
in years |
all age 80+
coded as 80
|
| SEX
|
1=male 2=female |
1=male
2=female
|
| RC7G
|
internet for non-grocery
shopping
|
1=yes 0=no |
| RC7E
|
internet for grocery shopping |
1=yes 0=no
missing if no internet use
|
| GROC
|
internet for grocery shopping
(missings recoded from RC7E)
|
1=yes 0=no or
no internet use
|
| PSU
|
primary sampling unit |
ids have been scrambled
|
| EMP_STA
|
current employment status |
see
codebook |
| GROUPINC |
grouped income data |
see
codebook |
| IND_WT |
weight variable for random
adult
|
scaled to add
to sample size
|
| GROSSWT |
ind_wt rescaled to sum to 2001
census totals for population aged 16+
|
sum of weights
is 4,089,946
|
| STRATUM |
stratum identifier based on local
authorities and mosaic groups
|
IDs have been
scrambled and do not now mean anything
|
NOTE ON VARIABLE NAMES:
Some of the programs we are using are case sensitive (R and
Stata)
- In Stata the variables names are all lower case.
- In R they are the elements of a data frame called shs
(lower case), but the elements of the data frame are upper
case e.g shs$UNIQID.
|
|
� |
|
P|E|A|S project 2004/2005/2006
|
|