N
-
Nagelkerkes R square
This is an adapted version of the R2 (coefficient of determination) that can be used in logistic regression. It approximates the proportion of the total variance in the data that the model accounts for (ranging from 0 to 1). It is produced by SPSS output when performing a logistic regression.
-
Natural Logarithm
Luckily, for our purposes at least, you do not need to know much about the natural logarithm (log). It is basically the logarithm to the base 'e' (2.718 to 3 d.p., a number of mathematical significance, like Pi). It has very useful properties for the purpose of logistic regression. See LGR module 4.2-4.4.
It looks like this:
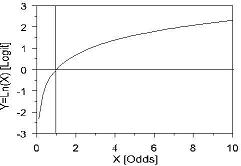
-
Nominal
Nominal variables are categorical and cannot be placed into any meaningful order. For example, gender and ethnicity may be coded numerically but the numbers do not indicate more or less of any quantity, these values serve only to represent the names of the category (e.g. White British=0, Mixed heritage=1, Indian=2, Pakistani=3 etc.) This can
be
contrasted with ordinal and continuous variables where the numerical codes do indicate amount of something e.g. on a Likert scale Strongly Agree (5) represents greater agreement with the statement than Strongly Diagree (1).
-
Normal distribution
A normal distribution is a distribution of data that clusters around the mean. When presented on a histogram the graph has a peak and a 'bell' shaped appearance. Normally distributed data is known to have specific properties which allow us to make inferences and is therefore very useful for statistical analysis! Many assumptions in regression
analysis revolve around 'normality' of data. The histogram below shows an example of normally distributed data:
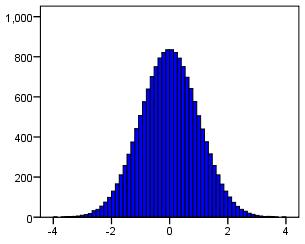
-
Null Hypothesis
- This is the opposite of your Alternative hypothesis and therefore states that your prediction is wrong (it usually states that there is no effect or relationship). Your research will aim to gather sufficient evidence to reject this null hypothesis.
|

