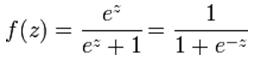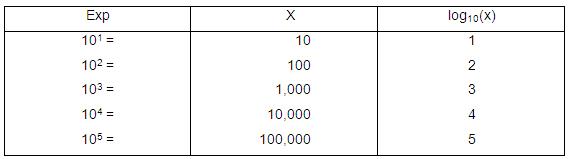
Consider the simple function bⁿ=X. The number b refers to the base, the number n is called the exponent and the result is the value X. The expression is known formally as exponentiation of b by n, but it is more commonly expressed as "b to the power n". For example 10³ is 10 raised to the power of 3 , or 10 * 10 * 10 =1000.

The log is the inverse function of the exponent. It can be applied to the value X to determine the exponent (n) at a given base. So to find the exponent (n) that raises b to give a specific value of X, we take the Log of X. Thus log_b (X) = n. So for example Log₁₀(1000) = 3.

Logs and exponents are therefore inverse functions of each other. This can be seen easily from the table below (Figure E1).

Figure E1: Log and Exponent Values

As log(x) increases by 1 the value of x increases by multiples of 10. So an increase of 1 in the log increases x by a factor of 10, an increase of 2 in the log increases X by a factor of 100 (10 * 10), an increase of 3 in the log increase x by a factor of 1000 (10 * 10 * 10) and so on. The key fact to extract here is that increasing X by multiples of a base value is equivalent to adding logs. This allows us to translate multiplication into addition of logarithms.

The natural log is the one where the base is approximately 2.718. This base has mathematical properties that make it useful in a variety of situations relating to calculus. Logarithms can be defined to any positive base other than 1, not just e, as logarithms in other bases differ only by a constant multiplier from the natural logarithm. In this module we are always using the natural logarithm (base e). The natural logarithm is generally written as ln(x), log_e(x) or sometimes, if the base e is implicit (as it is here), simply log(x).

An important fact about logs, in terms of logistic regression, is that because they represent powers of a base value (as we see in the above table) this allows us to translate multiplication into addition of logarithms. Two properties follow from this, namely:

1. log (x * y) = log x + log y.

2. log (x / y) = log x - log y.

This means the logistic regression equation can be linear and additive for the logged odds:

Log [p/(1-p)]= a + b₁x₁+ b₂x₂ etc.

but multiplicative for the odds:

p/(1-p)= Exp(a) * Exp(b₁x₁) * Exp (b₂x₂) etc.

This is why the regression coefficients (b) can be interpreted in terms of odds ratios, by taking the exponential of the log odds [Exp(b)].

 

What is the logistic function?

An explanation of logistic regression begins with an explanation of the logistic function:

 

The input is z and the output is ƒ(z). The logistic function is useful because it can take as an input any value from negative infinity to positive infinity, whereas the output is confined to values between 0 and 1. The variable e is the base of the natural logarithms (approximately 2.718). The variable z represents a set of explanatory variables, while ƒ(z) represents the probability of a particular outcome, given that set of explanatory variables. In the logistic regression context z is a linear combination of explanatory variables that predict the log odds:

z= a + b₁x₁+ b₂x₂ + b₃x₃ + ... + b_nx_n

where a is the intercept and b1, b2, b3 to b_n are the regression coefficients of the explanatory variables x₁, x₂ x₃ to x_n respectively. ‘z’ is the log odds of the event occurring.

Navigation

Home
Modules
Site Guide
Module 4 Contents
Resources